|
Dieses Resultat läßt sich auch anders
formulieren: Die Primzahlfunktion
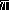 (x),
die die Anzahl der Primzahlen
kleiner als x angibt, strebt gegen Unendlich, falls
dies auch für
x gilt. Ein genaueres
Verhalten der Funktion (x),
die die Anzahl der Primzahlen
kleiner als x angibt, strebt gegen Unendlich, falls
dies auch für
x gilt. Ein genaueres
Verhalten der Funktion 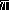 (x)
lag lange Zeit im Dunkeln. Gauß vermutete bereits als
Fünfzehnjähriger
(1792), daß sich der Quotient (x)
lag lange Zeit im Dunkeln. Gauß vermutete bereits als
Fünfzehnjähriger
(1792), daß sich der Quotient 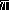 (x)
/ (x/log x) dem Wert 1 beliebig
nähert, wenn x gegen
Unendlich strebt. Doch erst 1896 konnte dieses Ergebnis bewiesen
werden.
Dieser sogenannte Primzahlsatz
läßt sich auch statistisch
interpretieren: Die Wahrscheinlichkeit für eine
natürliche Zahl
der Größenordnung x, eine
Primzahl zu sein, ist ungefähr
1/log x, d.h. in einem Intervall um x
der Länge a
liegen etwa a/log x Primzahlen. (Damit dies
statistisch sinnvoll
ist, sollte a genügend groß,
aber klein im Vergleich
zu x sein.) Entsprechend ist die Wahrscheinlichkeit
dafür,
daß zwei zufällig (in der Umgebung von x)
gewählte
Zahlen beide Primzahlen sind, etwa 1/(log x)2.
Bezogen
auf Primzahlzwillinge, d.h. Paare von Primzahlen,
deren Differenz
2 ist, bedeutet dies, daß in
Intervallen der genannten Art
a/(log x)2
Primzahlzwillinge zu erwarten sind. (In Wirklichkeit
etwas mehr, da die Tatsache, daß n prim
ist, die Wahrscheinlichkeit
für n+2, prim zu sein, verändert
(z.B. ist n+2
dann sicher ungerade).) Heuristische Überlegungen
führen zur Formel (x)
/ (x/log x) dem Wert 1 beliebig
nähert, wenn x gegen
Unendlich strebt. Doch erst 1896 konnte dieses Ergebnis bewiesen
werden.
Dieser sogenannte Primzahlsatz
läßt sich auch statistisch
interpretieren: Die Wahrscheinlichkeit für eine
natürliche Zahl
der Größenordnung x, eine
Primzahl zu sein, ist ungefähr
1/log x, d.h. in einem Intervall um x
der Länge a
liegen etwa a/log x Primzahlen. (Damit dies
statistisch sinnvoll
ist, sollte a genügend groß,
aber klein im Vergleich
zu x sein.) Entsprechend ist die Wahrscheinlichkeit
dafür,
daß zwei zufällig (in der Umgebung von x)
gewählte
Zahlen beide Primzahlen sind, etwa 1/(log x)2.
Bezogen
auf Primzahlzwillinge, d.h. Paare von Primzahlen,
deren Differenz
2 ist, bedeutet dies, daß in
Intervallen der genannten Art
a/(log x)2
Primzahlzwillinge zu erwarten sind. (In Wirklichkeit
etwas mehr, da die Tatsache, daß n prim
ist, die Wahrscheinlichkeit
für n+2, prim zu sein, verändert
(z.B. ist n+2
dann sicher ungerade).) Heuristische Überlegungen
führen zur Formel
|
C · a/(log x)2
mit C=1,3203236316...
für die Anzahl der Primzahlzwillinge zwischen x
und x+a.
Numerische Rechnungen liefern überraschende
Übereinstimmungen
mit der Theorie, überraschend insbesondere für
Primzahlzwillinge,
da noch nicht einmal bekannt ist, ob unendlich viele Primzahlzwillinge
existieren.
Primzahltest - Herausforderung für schnelles
Rechnen
Die Primzahlen gehören trotz ihrer einfachen
Definition zu den
willkürlichsten und widerspenstigsten Objekten der Mathematik.
Sie
scheinen keinem anderen Gesetz als dem Zufall unterworfen, und es gibt
keine Formel, aus der man ablesen kann, ob eine Zahl N
einePrimzahl
ist oder nicht. Gewiß, diese Entscheidung
läßt sich herbeiführen,
indem man N nacheinander versuchsweise durch jede
Primzahl teilt,
die kleiner als Wurzel aus N ist. Geht keine dieser
Divisionen auf,
ist N eine Primzahl. Der gravierendste Nachteil
dieser Methode:
Um mit ihr eine 100-stellige Zahl zu prüfen, braucht der
schnellste,
zur Zeit verfügbare Prozessor im ungünstigsten Fall
mehr als
1036 Jahre.
|
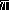 (x),
die die Anzahl der Primzahlen
kleiner als x angibt, strebt gegen Unendlich, falls
dies auch für
x gilt. Ein genaueres
Verhalten der Funktion
(x),
die die Anzahl der Primzahlen
kleiner als x angibt, strebt gegen Unendlich, falls
dies auch für
x gilt. Ein genaueres
Verhalten der Funktion 

